Matricez

MATRICES

RESEÑA HISTÓRICA
El origen de las matrices es muy antiguo. Los cuadrados latinos y los cuadrados mágicos se estudiaron desde hace mucho tiempo. Un cuadrado mágico, 3 por 3, se registra en la literatura china hacia el 650 a. C.
Es larga la historia del uso de las matrices para resolver ecuaciones lineales. Un importante texto matemático chino que proviene del año 300 a. C. a 200 a. C., Nueve capítulos sobre el Arte de las matemáticas (Jiu Zhang Suan Shu), es el primer ejemplo conocido de uso del método de matrices para resolver un sistema de ecuaciones simultáneas. En el capítulo séptimo, "Ni mucho ni poco", el concepto de determinante apareció por primera vez, dos mil años antes de su publicación por el matemático japonés Seki Kōwa en 1683 y el matemático alemán Gottfried Leibniz en1693.
Los "cuadrados mágicos" eran conocidos por los matemáticos árabes, posiblemente desde comienzos del siglo VII, quienes a su vez pudieron tomarlos de los matemáticos y astrónomos de la India, junto con otros aspectos de las matemáticas combinatorias. Todo esto sugiere que la idea provino de China. Los primeros "cuadrados mágicos" de orden 5 y 6 aparecieron en Bagdad en el 983, en la Enciclopedia de la Hermandad de Pureza (Rasa'il Ihkwan al-Safa).
Después del desarrollo de la teoría de determinantes por Seki Kowa y Leibniz para facilitar la resolución de ecuaciones lineales, a finales del siglo XVII, Cramer presentó en 1750 la ahora denominada regla de Cramer. Carl Friedrich Gauss y Wilhelm Jordan desarrollaron la eliminación de Gauss-Jordan en el siglo XIX.
Fue James Joseph Sylvester quien utilizó por primera vez el término « matriz » en 1848/1850.

En 1853, Hamilton hizo algunos aportes a la teoría de matrices. Cayley introdujo en 1858 la notación matricial, como forma abreviada de escribir un sistema de m ecuaciones lineales con n incógnitas.





Cronología

Año
Acontecimiento

200 a.C.
En China los matemáticos usan series de números.

1848 d.C.
J. J. Sylvester introduce el término "matriz".

1858
Cayley publica Memorias sobre la teoría de matrices.

1878
Frobenius demuestra resultados fundamentales en álgebra matricial.

1925
Werner Heisenberg utiliza la teoría matricial en la mecánica cuántica

CLASES DE MATRICES

Matriz fila
Una matriz fila está constituida por una sola fila.


Matriz columna
La matriz columna tiene una sola columna

Matriz rectangular
La matriz rectangular tiene distinto número de filas que de columnas, siendo su dimensión mxn.





Matriz traspuesta
Dada una matriz A, se llama matriz traspuesta de A a la matriz que se obtiene cambiando ordenadamente las filas por las columnas.

Matriz nula
En una matriz nula todos los elementos son ceros.



Matriz cuadrada
La matriz cuadrada tiene el mismo número de filas que de columnas.
Los elementos de la forma aii constituyen la diagonal principal.
La diagonal secundaria la forman los elementos con i+j = n+1, siendo n el orden de la matriz.

Tipos de matrices cuadradas
Matriz triangular superior
En una matriz triangular superior los elementos situados por debajo de la diagonal principal son ceros.

Matriz triangular inferior
En una matriz triangular inferior los elementos situados por encima de la diagonal principal son ceros.



Matriz diagonal
En una matriz diagonal todos los elementos que no están situados en la diagonal principal son nulos.


Matriz escalar
Una matriz escalar es una matriz diagonal en la que los elementos de la diagonal principal son iguales.



Matriz identidad o unidad
Una matriz identidad es una matriz diagonal en la que los elementos de la diagonal principal son iguales a 1.

DEFINICIÓN DE MATRICES

Se puede definir una matriz, como un conjunto de elementos (números) ordenados en filas y Columnas.
Para designar una matriz se emplean letras mayúsculas. Cada uno de los elementos de la matriz (aij) tiene dos subíndices. El primero i indica la fila a la que pertenece y el segundo j la columna.
Esta es una matriz de m filas y n columnas, es decir, de dimensión m x n. Esta matriz también se puede representar de la forma siguiente: A = (aij) m x n. Si el número de filas y de columnas es igual ( m = n ), entonces se dice que la matriz es de orden n.

IGUALDAD DE MATRICES

Dos matrices son iguales cuando tienen la misma dimensión y los elementos que ocupan la misma posición en ambas son iguales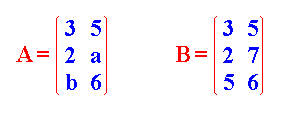
Para que las matrices A y B sean iguales, se tiene que cumplir que a = 7 y b = 5.

Operaciones entre matrices

Suma y diferencia de matrices

Producto por un escalar por una matriz

Producto de matrices
Mm x n x Mn x p = M m x p

Determinantes

A cada matriz cuadrada A se le asigna un escalar particular denominado determinante de A , denotado por |A| o por det (A).
Método para encontrar la determinante de una matriz



Determinante de orden uno
|a11| = a11
Ejemplo
|−2| = −2
Determinante de orden dos

= a 11 a 22 − a 12 a 21
Ejemplo